mandag 11. februar 2019 Go Bøker
Jeg fortsetter å lese Mazes for Programmers og å leke meg med labyrinter. Om dette kommer som en stor overraskelse så vil du kanskje lese min forrige blogpost først: Generere labyrinter (i Go).

Siden forrige gang har jeg gjort en hel del; jeg har laget et prosjekt rundt koden min, og du finner det på github.com/tormaroe/maze. Mazes for Programmers har vært akkurat så gøy og så lærerikt som jeg hadde håpet, og har gitt meg en flott anledning til å praktisere Go-programmering.
Og om du har Go på maskinen din kan du enkelt laste ned, bygge og installere programmet mitt med denne kommandoen:
$ go get github.com/tormaroe/maze
Etter dette skal du kunne kjøre maze. Nå kan du for eksempel skrive ut en random labyrint i terminalen ved å kjøre følgende kommando:
$ maze ascii sidewinder --height 10 --width 20 --random
For å genere en labyrint i PNG format med fine farger kan du gjøre noe sånt som dette:
$ maze png huntandkill --seed 42 -cv -o mymaze.png
Kjør maze --help for mer info om valgmulighetene.
I resten av denne blogposten presenterer jeg de ulike algoritmene som programmet mitt implementerer for å generere labyrinter. Fargeleggingen, og det å finne den lengste stien i labyrinten, er basert på Dijkstra's algoritme, som vi bruker til å kalkulere distansen fra et punkt til alle andre punkt. Forskjellen i fargetone i de fargede labyrint-bildene viser hvor langt to punkt er fra hverandre, og det avslører strukturen i labyrintene på en interessant måte.

Boken beskriver binary tree som den enkleste algoritmen for å generere en labyrint. Som du kan se gir den labyrinter som tydelig tenderer mot korridorer i en bestemt retning, og i tillegg får man alltid en lang korridor på to av sidene. På den andre siden har algoritmen lineær kjøretid - man trenger bare loope over alle cellene én gang.
Her er implementasjonen min i Go:
func (g *Grid) BinaryTreeMaze() {
g.eachCell(func(c *Cell) {
neighbors := make([]*Cell, 0, 2)
if c.north != nil {
neighbors = append(neighbors, c.north)
}
if c.east != nil {
neighbors = append(neighbors, c.east)
}
if len(neighbors) > 0 {
index := rand.Intn(len(neighbors))
neighbor := neighbors[index]
c.link(neighbor)
}
})
}
Sidewinder er egentlig like enkel som binary tree, bare at den er mer random i én retning. Resultatet ser du er at vi står igjen med én lang korridor i stedet for to, og at tendensen til hvor korridorene går har endret seg.
Her følger min implementasjon:
func (g *Grid) SidewinderMaze() {
g.eachRow(func(row []*Cell) {
run := make([]*Cell, 0, len(row))
for _, c := range row {
run = append(run, c)
atEastBound := c.east == nil
atNorthBound := c.north == nil
shouldClose := atEastBound || (!atNorthBound && coinflip())
if shouldClose {
member := sample(run)
if member.north != nil {
member.link(member.north)
}
run = make([]*Cell, 0, len(row))
} else {
c.link(c.east)
}
}
})
}

Aldous-Broder, oppkalt etter David Aldous og Andrei Broder som kom opp med den hver for seg, gir en labyrint helt uten slike tendenser som vi har sett i de to firrige algoritmene. Algoritmen gir en gjevn fordeling av tilfeldighet.
Aldous-Broder har derimot en helt annen kjøretid. Den "beveger seg" tilfeldig gjennom griddet og forsøker å finne passasjer å åpne. Etterhvert blir det vanskeligere og vanskeligere, og i teorien er det ikke sikkert den vil klare å gjøre seg ferdig i det hele tatt. I praksis derimot opplever jeg at jeg kan generere svære labyrinter med min Go-implementasjon på null-komma-swish.
func (g *Grid) AldousBroderMaze() {
cell := g.randomCell()
unvisited := g.size() - 1
for unvisited > 0 {
neighbor := sample(cell.neighbors())
if len(neighbor.links) == 0 {
cell.link(neighbor)
unvisited--
}
cell = neighbor
}
}
Jeg hopper over en algoritme fra boken som kalles Wilson's algoritme. Den gir det samme resultatet som Aldous-Broder, men der hvor sistnevnte bruker relativt sett lang tid å avslutte så bruker Wilson's lang tid på å komme i gang. En interessant ting man kan forsøke om man vil eksperimentere litt er å kombinere de to algoritmene; starte med Aldous-Broder og avslutte med Wilson's.

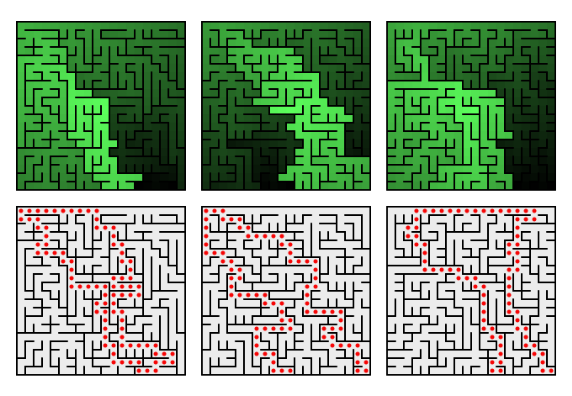
Til slutt har jeg implementert en algoritme labyrint-boken kaller Hunt-and-kill. Den gir ikke en så gjevn distribusjon av tilfeldighet som Aldous-Broder. Derimot tenderer den til å gi lengre korridorer og færre blindveier. Det betyr også at den lengste stien typisk er lengre i Hunt-and-kill-labyrinter.
De lengste stiene i labyrintene over er i snitt 110 celler lange, mens for eksempel Aldous-Broder hadde et snitt på 84.
Her er min implementasjon av Hunt-and-kill:
func (g *Grid) HuntAndKillMaze() {
current := g.randomCell()
for current != nil {
unvisitedNeighbors := filter(current.neighbors(), func(c *Cell) bool {
return len(c.links) == 0
})
if len(unvisitedNeighbors) > 0 {
neighbor := sample(unvisitedNeighbors)
current.link(neighbor)
current = neighbor
} else {
current = nil
g.eachCell(func(c *Cell) {
visitedNeighbors := filter(c.neighbors(), func(n *Cell) bool {
return len(n.links) > 0
})
if len(c.links) == 0 && len(visitedNeighbors) > 0 {
current = c
neighbor := sample(visitedNeighbors)
current.link(neighbor)
}
})
}
}
}