onsdag 19. oktober 2011 Polyglot Ruby Prolog Kata
I forrige uke hadde jeg en litt spesiell Coding Dojo / ZipTalk på jobben. Jeg startet med å gi utviklerne på teamet en oppgave, og sa at de hadde en halv time til å komme opp med en løsning i felleskap. Oppgaven er hentet fra Structure and Interpretation of Computer Programs (hvor den ble brukt til å illustrere ikke-deterministisk programmering), og lød som følger:
Baker, Cooper, Fletcher, Miller og Smith bor i samme hus med fem etasjer, men i hver sin etasje. Baker bor ikke i øverste etasje, og Cooper bor ikke nederst. Fletcher bor hverken øverst eller nederst. Miller bor høyere opp enn Cooper. Smith bor ikke i etasjen direkte over eller under Fletcher. Fletcher bor ikke i etasjen direkte over eller under Cooper.
Lag et program som forteller i hvilken etasje hver av dem bor!
Hvis du ønsker å forsøke deg på oppgaven selv anbefaler jeg at du gjør det før du leser videre!
Jeg kastet med vilje utviklerne ut på dypt vann, og hadde ikke regnet med at de ville komme i mål. Noe de heller ikke gjorde. Målet mitt med oppgaven var blant annet å gi dem erfaring med å kaste seg over en oppgave under sterkt tidspress, og se hvordan de sammarbeidet. Men det var også å presentere en alternativ måte å løse slike oppgaver på – mer om det litt lenger nede.
Da halvtimen var over snakket vi litt om oppgaven og hvordan det hadde gått, og så presenterte jeg et par løsninger på problemet i Ruby. Den første er ikke spesielt elegant, men fungerer. Prinsippet er at jeg ved hjelp av fem nøstede for-løkker genererer alle mulige kombinasjoner av etasjer for de fem beboerne. I den innerste løkken skipper jeg løsninger som ikke er korrekte i forhold til reglene i oppgaven ved å bruke next (samme som continue i C# og andre steder).
Til slutt skriver jeg ut de akseptable løsningene. Her følger koden:
10 for baker in 1..5 11 for cooper in 1..5 12 for fletcher in 1..5 13 for miller in 1..5 14 for smith in 1..5 15 all = [baker, cooper, fletcher, miller, smith] 16 next unless all.count(1) == 1 17 next unless all.count(2) == 1 18 next unless all.count(3) == 1 19 next unless all.count(4) == 1 20 next unless all.count(5) == 1 21 22 next if baker == 5 23 next if cooper == 1 24 next if fletcher == 1 or fletcher == 5 25 next unless miller > cooper 26 next if (smith - fletcher).abs() == 1 27 next if (fletcher - cooper).abs() == 1 28 29 puts "Baker = #{baker}" 30 puts "Cooper = #{cooper}" 31 puts "Fletcher = #{fletcher}" 32 puts "Miller = #{miller}" 33 puts "Smith = #{smith}" 34 puts 35 end 36 end 37 end 38 end 39 end
Deretter demonstrerte jeg en løsning hvor jeg utnytter litt flere av Ruby's muligheter. I linje 10 til 16 nedenfor monkey-patcher jeg Array-klassen med litt syntakstisk sukker for å gjøre løsningen mere lesbar. Linje 27 til 34 skriver ut de gyldige løsningene.
Selve løsningen på problemet ligger i linje 18 til 25. Her bruker jeg permutation-metoden til å gi meg alle kombinasjonene av et array – det tilsvarer de 10 første linjene i løsningen over. Deretter bruker jeg find_all (tilsvarer filter i mange andre språk) til å begrense permutasjonene til de som er gyldige.
10 class Array 11 def baker; self[0] end 12 def cooper; self[1] end 13 def fletcher; self[2] end 14 def miller; self[3] end 15 def smith; self[4] end 16 end 17 18 answer = [1,2,3,4,5].permutation.find_all do |solution| 19 not solution.baker == 5 and 20 not solution.cooper == 1 and 21 not solution.fletcher == 1 and not solution.fletcher == 5 and 22 solution.miller > solution.cooper and 23 not (solution.smith - solution.fletcher).abs() == 1 and 24 not (solution.fletcher - solution.cooper).abs() == 1 25 end 26 27 answer.each do |a| 28 puts "Baker = #{a.baker}" 29 puts "Cooper = #{a.cooper}" 30 puts "Fletcher = #{a.fletcher}" 31 puts "Miller = #{a.miller}" 32 puts "Smith = #{a.smith}" 33 puts 34 end
Men poenget mitt med denne CodingDojoen/ZipTalken var å introdusere noe helt annet...
Prolog er et logisk programmeringsspråk. I motsetning til Ruby, som er imperativt, er logiske språk deklerative. Det vil si at i stedet for å implementere en algoritme for å løse problemet så beskriver vi bare selve problemet, og Prolog løser det for deg!
Prolog kan se ganske gresk ut for dem som ikke har vært borti det før, men la oss bare hoppe i det. Jeg skal forsøke å forklare underveis.
1 apartments([]). 2 apartments([Head|Tail]) :- 3 member(Head, [1,2,3,4,5]), apartments(Tail).
Linjene over er en regel som forteller Prolog hva en liste av leiligheter/etasjer er for noe. Linje 1 sier at en tom liste, alstå [], er en liste av leiligheter. De neste to linjene er en rekursiv regel som sier at en ikke-tom liste er en liste av leiligheter om det første elementet (Head) er et medlem av listen [1,2,3,4,5], og resten av elementene (Tail) også er en gyldig liste av leiligheter.
Tok du den?
5 distinct([]). 6 distinct([Head|Tail]) :- 7 \+member(Head, Tail), distinct(Tail).
Linje 5 til 7 beskriver regelen som sier at alle må bo i forskjellige etasjer – altså at løsningen må være en liste hvor alle elementene er unike. Først sier jeg at en tom liste er ok. Deretter sier jeg at en ikke-tom liste er ok om det første elementet (Head) ikke finnes i resten av elementene (Tail), og resten av elementene også er en unik liste. Backslash og pluss betyr "ikke" i Prolog.
I den neste linjen lager jeg for enkelhets skyld en regel som kombinerer de to forrige reglene:
9 distinct_apartments(L) :- apartments(L), distinct(L).
Og så er det på tide å fortelle Prolog hva det vil si å bo rett over eller rett under en annen beboer. I linje 11 og 12 sier jeg at X og Y bor i tilstøtende etasjer hvis absoluttverdien av X minus Y (som jeg kaller Diff) er lik 1.
11 adjacent(X, Y) :- 12 Diff is abs(X - Y), Diff = 1.
Da gjenstår det bare å lage en hovedregel som inkluderer alle detaljene fra oppgaven. I dwelling sier jeg at Baker, Cooper, Fletcher, Miller og Smith bor i hver sin etasje, at Baker ikke bor i femte, at Cooper ikke bor i første, at Fletcher hverken bor i femte eller første, at Miller bor høyere opp enn Cooper, og at Smith og Fletcher, og Fletcher og Cooper ikke bor like over eller under hverandre.
14 dwelling(Baker, Cooper, Fletcher, Miller, Smith) :- 15 distinct_apartments([Baker, Cooper, Fletcher, Miller, Smith]), 16 Baker \= 5, 17 Cooper \= 1, 18 Fletcher \= 1, Fletcher \= 5, 19 Miller > Cooper, 20 \+adjacent(Smith, Fletcher), 21 \+adjacent(Fletcher, Cooper).
Og da er vi ferdige. Fyrer jeg opp Prolog og kjører regelen min så får jeg svaret:
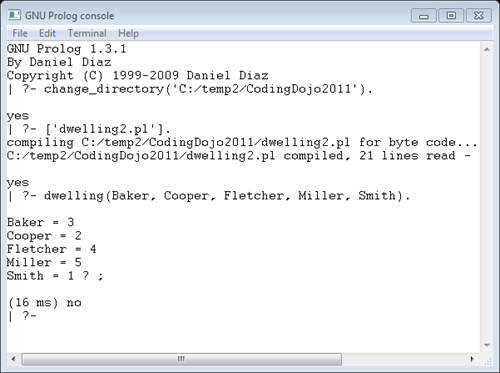
Prolog sier helt til slutt "no" fordi jeg spurte om det fantes flere løsninger – og det gjorde det ikke.
Poenget var at med Prolog så har jeg ikke behøvd å tenke på hvordan jeg skulle løse oppgaven algoritmisk. Jeg har ikke behøvd å generere en masse forslag til løsninger som jeg så må filtrere. I stedet har jeg bare reformulert oppgaven på en måte som Prolog forstår, og Prolog finner selv den korrekte løsningen for meg.
Det er dette vi kaller deklerativ programmering.
Da teamet forsøkte å løse oppgaven under sterkt tidspress klarte de ikke å komme opp med den nødvendige algoritmen. Om de hadde kunnet Prolog hadde de ikke behøvd det. Er ikke det ganske interessant?
For de som er interessert i Coding Dojo konseptet vil jeg benytte anledningen til å nevne at det i disse dager er tatt initiativ til en CodingDojo i Bergen. Det er Kjerti Berg som jobber i konsultenselskapet Miles som står bak. Og målet er at folk som ønsker å bli bedre programmerere skal få øve sammen med likesinnede gjennom kode kataer i en sosial setting.
Det første møtet blir 22. november. Kommer du?
Relaterte innlegg: Coding Dojo på Contiki, ZipTalks på jobben.