torsdag 25. mars 2010 Polyglot
Jeg har tidligere snakket om betydningen av å beherske både statiske og dynamiske språk. En annen akse blivende polygloter er nødt til å se nærmere på er det vi kaller ulike programmeringsparadigmer.
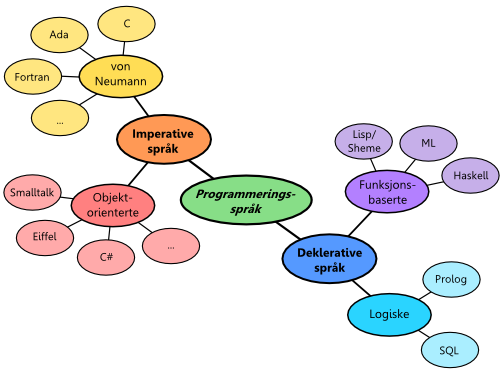
(Språk-treet er selvfølgelig ikke komplett, og kategoriseringen er åpen for diskusjon.)
Om du har omtrent samme bakgrunn som meg er du mest kjent med de imperative språkene, som dominerer software-bransjen. Imperativ (eller befalende om du vil) betyr at vi forteller datamaskinen detaljert hva den skal gjøre - vi manipulerer variabler for å oppnå ønsker resultat.
Jeg tror det er veldig viktig at vi også studerer og lærer oss å beherske de mere deklerative (eller beskrivende) språkene. De tvinger oss til å tenke ganske anderledes når vi skal løse problemer. Om vi til syvende og sist likevel benytter oss av et imperativt språk så vil det vi lærer gi oss nye perspektiv som hjelpe oss til å løse oppgavene våre bedre. Dessuten er det mange språk som befinner seg i flere kategorier samtidig, som støtter f.eks. både objektorientering og funksjonsorientering (som alltid er det glidende overganger).
For å illustrere forskjellene mellom et utvalg paradigmer skal vi se på ulike løsninger for å finne den største, felles divisoren mellom to tall (heretter kalt gcd - Greatest common divisor). Og vi begynner med det vi kjenner best…
Den imperative algoritmen er for anledningen implementert i C, og illustrerer hvordan befalende kode fungerer:
For å beregne gcd av a og b, undersøk om a og b er like. Hvis så er tilfelle, returner en av dem. Hvis ikke, bytt den største av dem med forskjellen mellom dem og repeter.
I et funksjonelt språk som Scheme legger man vekt på det matematiske forholdet mellom input og output. Lambda-nøkkelordet introduserer en definisjon av en funksjon, og (a b) er funksjonens argumentliste. "cond" er en slags switch/case-konstruksjon. (- a b) er et kall til metoden "-" (minus) med a og b som argumenter. Her er metoden i pseudokode:
Gcd av a og b er definert til å være (1) a når a og b er like, (2) gcd av b og a – b når a er større enn b, og (3) gcd av a og b – a når b er større enn a. For å beregne gcd for to numre, ekspander og forenkle denne definisjonen til avslutning.
Rekursjon er en av hovedvirkemidlene i funksjonsbasert programmering. Samme algoritme kunne man selvsagt ha fått til i imperative språk også, selv om det er vanligere å se den første varianten. Det er derimot mye fra imperativ programmering man ikke gjør i funksjonsbasert. Fraværet av (det vi for enkelhets skyld kan kalle) variabel-manipuleringen gjør at funksjonsbasert kildekode i større grad kan analyseres for korrekthet. Det er også enklere å automatisere enkelte optimaliseringer, som å parallellisere programmer.
I et logisk språk spesifiserer vi et sett med axiomer og regler som lar systemet finne løsningen. Det kan være enklere å forstå Prolog-koden om du leser ":-" som "hvis" og "," som "og". Her er det samme i pseudokode:
Proposisjonen gcd(a, b, g) er sann om (1) a, b og g er alle like, (2) a er større enn b og det eksisterer et nummer c slik at c er lik a – b og gcd(c, b, g) er sant, eller (3) a er mindre enn b og det eksisterer et nummer c slik at c er lik b – a og gcd(c, a, g) er sant. For å beregne gcd av to numre, søk etter et nummer g (og ulike numre c) slik at man kan bevise at gcd(a, b, g) er sant.
Valget av imperativ, funksjonell eller logisk programmering får som sagt ikke bare betydning for hvordan koden blir seende ut, men også hvordan utvikleren tenker for å komme opp med en løsning. Å beherske disse måtene å tenke på vil gjøre deg til en bedre problemløser. I tillegg vil du ha flere verktøy å velge blant – noen problemer vil alltid være enklere å løse deklerativt enn imperativt.
En annen ting som er interessant med de deklerative språkene er at vi ikke tvinger datamaskinen til å jobbe på en bestemt måte. Det muligjør implementasjon av forbedringer uten å røre program-koden, f.eks. gjennom å utvikle bedre kompilatorer. Den samme effekten har vi f.eks. når vi benytter LINQ i .net; LINQ er et deklerativt subset av C#/VB.net.
Om du er Java-utvikler, eller C#-utvikler som meg, så skal du være klar over at du har tilgang til funksjonsbaserte språk på favorittplattformen din også. Scala på Java-plattformen er et språk som kombinerer objektorientering og funksjonsbasert programmering. Fra Microsoft har vi fått F#, en variant av ML som støttes fullt ut i Visual Studio 2010 – på samme måte som Scala kombinerer også F# den funksjonelle og den objektorienterte paradigmen.
Hvis du vil ha et språk som er "renere" kan du velge Clojure - en moderne (2007) Lisp-dialekt som kjører på både .Net og Java-plattformen. Er du interessert i logiske språk kan du ta en titt på P#, som gir deg Prolog i .net. Prolog Cafe er tilsvarende for Java.
For komplette lister over språk på Java Virtual Machine og Common Language Infrastructure, se her og her.
Denne blogposten var inspirert av boken Programming Language Pragmatics, hvor kodesnuttene også er sakset fra.