fredag 20. september 2013 Polyglot CoffeeScript Lambda
Det er lurt å lese del 1 om boolske variabler og del 2 om tall før du tar fatt på denne posten...
I del to definerte vi funksjonen INCREMENT, og i denne delen skal vi gå videre med å definere flere numeriske operasjoner.
Noe av det første vi lærer på skolen er å plusse sammen to tall, så det kan jo være en grei funksjon å ha. Og den er ganske enkel å lage så lenge vi husker hva et tall er i lambda calculus: Nemlig en funksjon som kaller sitt første argument så mange ganger som tallet tilsier. Dermed får vi:
ADD = (m) -> (n) -> n(INCREMENT)(m)
som betyr at m + n er det samme som m inkrementert n ganger. Dermed vil for eksempel
show toNumber(ADD(THREE)(FOUR))
skrive ut tallet "7" fordi 3 + 4 = 3 + 1 + 1 + 1 + 1 = 7. Easy peasy lemon squeezy!
Når vi har laget pluss blir det også enkelt å gange to tall:
MULTIPLY = (m) -> (n) -> n(ADD(m))(ZERO)
Her sier vi altså at m * n er det samme som om vi starter med 0 (ZERO) og n ganger plusser på m. For eksempel er 3 * 4 = 0 + 3 + 3 + 3 + 3 = 12.
Og når vi har MULTIPLY kan vi enkelt opphøye et tall i et annet tall.
POWER = (m) -> (n) -> n(MULTIPLY(m))(ONE)
m opphøyd i n er altså det samme som (litt upresist) n ganger 1 * m. 3 opphøyd i 4 er da for eksempel 1 * 3 * 3 * 3 * 3 = 81.
Å trekke et tall fra et annet tall er litt vanskeligere enn det vi har gjort sålangt. Hvorfor? Å øke et tall er enkelt fordi det kun krever flere funksjonskall. Skal vi redusere et tall må vi fjerne funksjonskall, og det kan vi ikke uten videre gjøre. Så hva gjør vi da?
Se for deg at vi kan lage par av tall.

Som alt annet i lambda calculus må et par være en funksjon. Vi definerer den slik:
PAIR = (x) -> (y) -> (f) -> f(x)(y)
Se på dette som en funksjon som tar i mot 2 argumenter (x og y) og returnerer en funksjon som kaller sitt argument (f) med x og y. Dermed kan vi lage to funksjoner for å aksessere disse to variablene:
LEFT = (p) -> p( (x) -> (y) -> x ) RIGHT = (p) -> p( (x) -> (y) -> y )
Se videre for deg at vi har en funksjon SLIDE som kan inkrementere et par av tall som i tegningen under. Ved å bruke dette kan vi holde track på hvilket tall som er ett mindre enn et gitt annet tall.
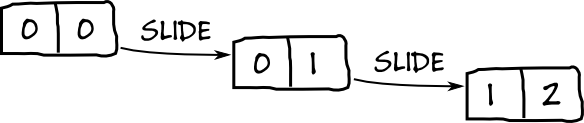
SLIDE definerer vi slik:
SLIDE = (p) -> PAIR(RIGHT(p))(INCREMENT(RIGHT(p)))
Og nå er det plutselig ikke så vanskelig å definere en funksjon som dekrementerer (trekker fra 1) fra et tall:
DECREMENT = (n) -> LEFT(n(SLIDE)(PAIR(ZERO)(ZERO)))
DECREMENT vil altså starte med paret (0,0) og "slide" tallet n ganger. Til slutt returnerer funksjonen venstresiden av paret. Endelig kan vi bruke DECREMENT til å implementere subtraksjon, akkurat som vi bruke INCREMENT til å implementere addisjon:
SUBTRACT = (m) -> (n) -> n(DECREMENT)(m)
I del 2 laget vi en funksjon for å kontrollere om et tall var lik 0. Nå som vi har DECREMENT i verktøykassen kan vi lage en ny funksjon som sjekker om et tall er mindre eller lik et annet tall. For m er mindre eller lik n hvis (m – n) er mindre eller lik 0:
IS_LESS_OR_EQUAL = (m) -> (n) -> IS_ZERO(SUBTRACT(m)(n))
Disclamer: I tall-systemet vi har laget finnes det ikke negative tall, og DECREMENT av 0 er lik 0. 3 minus 5 vil for eksempel derfor også bli 0.
show toBool(IS_LESS_OR_EQUAL(ONE)(TWO)) show toBool(IS_LESS_OR_EQUAL(TWO)(TWO)) show toBool(IS_LESS_OR_EQUAL(THREE)(TWO))
Linjene over skriver derfor ut "true", "true" og "false".
Jeg er nå klar for å implementere første versjon av modulo, funksjonen for å finne resten av et heltall eller en divisjon med et annet tall. Her er en fremgangsmåte basert på de byggestenene vi nå har:
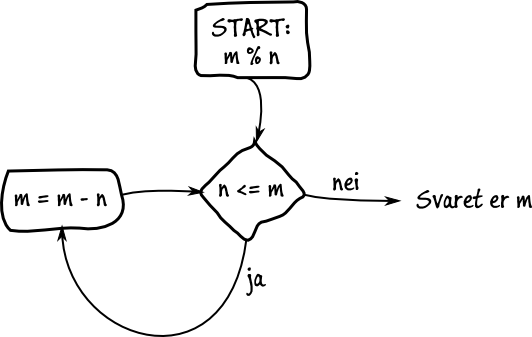
Og her er noen eksempler:
10 % 3 ==> m = 10 , n = 3, svar = ?
m = 10-3 = 7, n = 3, svar = ?
m = 7-3 = 4, n = 3, svar = ?
m = 4-3 = 1, n = 3, svar = m = 1
8 % 4 ==> m = 8 , n = 4, svar = ?
m = 8-4 = 4, n = 4, svar = ?
m = 4-4 = 0, n = 4, svar = m = 0
I min CoffeeScript-baserte lambda calculus kan denne algoritmen implementeres slik:
MOD = (m) -> (n) ->
IF(IS_LESS_OR_EQUAL(n)(m))(
(x) -> MOD(SUBTRACT(m)(n))(n)(x)
)(
m
)
Denne MOD-funksjonen fungerer. Jeg kan for eksempel kjøre
show toNumber(MOD(THREE)(TWO))
som skriver "1" til konsollet. Men definisjonen har et alvorlig problem – den bryter reglene i lambda calculus. Den bruker nemlig rekursjon: den kaller funksjonen MOD i definisjonen av MOD. Dette går ikke an, siden MOD-variabelen er noe jeg egentlig bare lager for å gjøre ting enklere for deg om meg. Skulle jeg gjort dette riktig måtte jeg ha erstattet "MOD" i definisjonen med implementasjonen av MOD. I den definisjonen måtte jeg gjort det samme, og jeg måtte ha fortsatt i det uendelige....
I neste post i denne serien må jeg fikse problemet med den rekursive MOD-funksjonen. For å gjøre det vil jeg introdusere deg for noe som kalles Z-kombinatoren. Den er nesten det samme som den mere kjente Y-kombinatoren, som du kanskje har hørt funksjonfolk snakke om.