søndag 21. april 2013 F# Trær Rekursjon

Hvis du aldri før har sett det jeg nå skal demonstrere, og du samtidig er klar til å forstå det, så kan du se frem til en ganske stor a-ha-opplevelse. Teknikken du vil få se er avansert og enkel på samme tid. Noen vil si det er trivielt, mens andre vil bruke lang tid på å skjønne det.
I denne posten vil jeg bruke F# til å presentere et problem med rekursiv traversering av tre-strukturer. Jeg vil så bruke continuation-passing style til å løse problemet.
I blogposten Funksjonell lek med trær i F# definerte jeg en generisk tre-datatype. Jag lagde en generell funksjoner som traverserte trærne, en slags fold eller reduce for trær.
Det jeg skal gjøre nå er omtrent det samme, men jeg har valgt å holde det enda enklere. Først definerer vi en type IntTree som brukes til å bygge trær. En node i treet er enten en bladnode som holder på et heltall, eller en node med to undernoder. Dette er altså et binærtre.
type IntTree =
| Leaf of int
| Node of IntTree * IntTree
Nå kan jeg bygge et tre på denne måten:
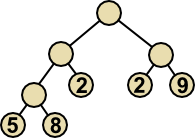
let tree = Node(Node(Node(Leaf 5,
Leaf 8),
Leaf 2),
Node(Leaf 2,
Leaf 9))
Tegner vi opp dette treet grafisk ser det slik ut:
Nå kan vi lage en summeringsfunksjon for slike trær. Dette er en enkelt, reksursiv funksjon som består av to regler:
En slik funksjon uttrykkes elegant i F#:
let rec sumTree tree =
match tree with
| Leaf n -> n
| Node (left, right) -> sumTree left
+ sumTree right
For å teste sumTree hopper jeg over i F# interactive:
> sumTree tree;; val it : int = 26
Summen rapporteres korrekt som 26.
sumTree har derimot én utfordring. Du ser at det er to rekursive kall for hver node, og at verdiene fra disse kallene plusses sammen. Vi har dermed ingen halerekursjon, og kontrollstacken vil vokse.
For små trær er ikke dette noe problem. Og godt balanserte trær kan inneholde mange elementer før treet blir dypt. Men sett at vi har et tre som ikke er så godt balansert.
La oss lage noen tall å jobbe med:
> let rnd = new System.Random();;
val rnd : System.Random
> let numbers =
List.init 100000 (fun _ -> rnd.Next(-50, 51));;
val numbers : int list =
[-46; -43; -22; -3; 20; 0; -43; -19; -50; 28; 35; -26; 20;
40; -4; -42; 5; 37; 27; -9; 28; 38; 29; 2; -23; -4; -29;
41; 10; 47; 39; -23; 37; 42; 12; -10; 1; -4; -39; ...]
numbers inneholder nå hundre tusen tall mellom –50 og 50. Jeg kan så konstuere et ubalansert tre basert på disse tallene:
> let imbalancedTree =
numbers |> List.fold (fun currentTree num ->
Node(Leaf num, currentTree)) (Leaf 0);;
val imbalancedTree : IntTree =
Node
(Leaf 49,
Node
(Leaf -3,
Node
(Leaf -38,
Node
(Leaf 42,
Node
(Leaf 11,
...
Dybden på imbalancedTree er nå hundre tusen. Hva skjer om jeg forsøker å summere tallene i dette treet?
> sumTree imbalancedTree;; Process is terminated due to StackOverflowException.
Jepp, der fikk vi en stack overflow! Den rekursive algoritmen måtte gjøre 100.000 kall til sumTree før den kunne plusse sammen høyre og venstre deltre, og hvert kall konsumerte en liten bit av stacken. Det går ikke!
Vi må finne på noe annet...
Begrepet Continuation-passing style (CPS) ble skapt av Gerald Jay Sussman og Guy L. Steele i 1975 da de begynte utviklingen av programmeringsspråket Scheme.
En funksjon skrevet i denne stilen tar ett ekstra argument: en "continuation", det vil si en funksjon. Når CPS-funksjonen har kalkulert sitt resultat "returnerer" den dette resultatet ved å kalle continuation-funksjonen med resultatverdien som argument.
Utviklere som bruker asynkrone API'er, for eksempel utviklere som programmerer for node.js, bruker mye callbacks – og det er egentlig CPS. Men teknikken har flere bruksområder. Nå skal jeg bruke CPS til å fikse problemet med den rekursive funksjonen sumTree.
Jeg skal lage en ny summeringsfunksjon. Den vil ha to parametre, og følgende signatur:
tree:IntTree -> cont:(int -> 'a) -> 'a
For dem som ikke er så vandt til å lese F#/ML/Haskell-signaturer:
tree er en instans av et IntTree
cont er en funksjon som tar inn en integer og returnerer en verdi av den generiske typen a
aOg her er den nye funksjonen:
let rec sumTreeCont tree cont =
match tree with
| Leaf n -> cont n
| Node (left, right) ->
sumTreeCont left (fun leftSum ->
sumTreeCont right (fun rightSum ->
cont (leftSum + rightSum)))
Til å begynne med ser funksjonen nokså lik ut, men når vi kommer til den rekursive delen tar det litt av. Jeg gjør et rekursivt kall for det venstre deltreet, og bygger en ny continutation som jeg sender med. I den nye continuation'en er det et nytt kall til summeringsfunksjonen for det høyre deltreet, og der sender jeg med den orginale continuation-funksjonen.
Har du sett slik kode før så er det ikke så vanskelig. Men om du ikke er kjent med dette så vil det sansynligvis ta litt tid å bygge opp en inuitiv følelse for hva som skjer her. Jeg har derfor forsøkt å lage en litt forenklet illustrasjon av hva som skjer om jeg skal summere tallene i et lite tre med bare én vanlig node og to bladnoder:
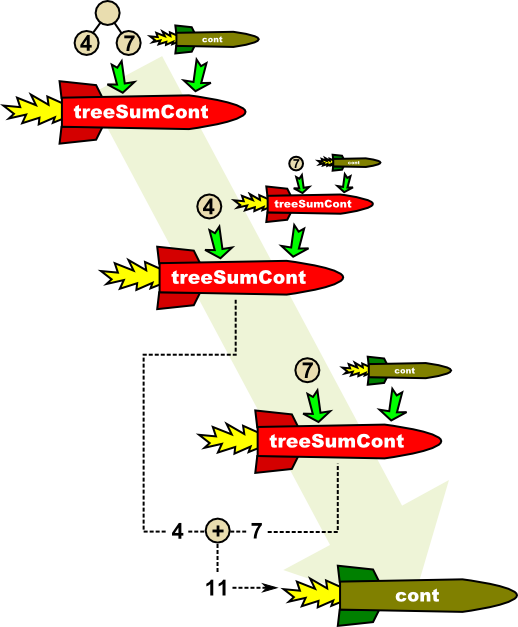
Rekursjonen her har fire "trinn". I trinn 2 ser du at vi bare jobber med bladnoden med verdien 4, men at vi tar vare på kalkulasjonen vi må utføre siden (summering av det høyre deltreet). Når venstre side er ferdig kan vi så utføre det vi har tatt vare på (trinn 3). Helt til slutt vil den orginale continuation-funksjonen bli evaluert.
Nå kan vi forsøke å summere tallene i det ubalanserte treet. Jeg sender med en continuation som vil ta summen og produsere en tekststreng som sier hva resultatet er (her bruker jeg partial application som jeg har snakket om mange ganger før).
> sumTreeCont imbalancedTree (sprintf "Result is: %d");; val it : string = "Result is: 8549"
Og denne gangen fungerte det. Summeringsfunksjonen bruker nå halerekursjon, og kompilatoren kan dermed optimalisere den til å ikke "spise opp stacken".
Det kan være vanskelig å få en god, intuitiv forståelse for hvordan algoritmer og funksjoner som bruker continuations fungerer. Men continuation-passing style kan løse utfordringer som det kan være svært vanskelig å løse på andre måter. Denne stilen har vært praktisert siden Vietnamkrigen (ingen sammenheng forøvrig), og jeg ser på det som en viktig teknikk som en komplett utvikler bør ha i verktøykassen sin.
PS: Denne blogposten er inspirert av boken Real-World Functional Programming (med eksempler i C# og F#).