fredag 25. november 2011 Julekalender Clojure Ruby
I forrige bloggpost presenterte jeg ulike løsninger på Euler-problem nummer 1. Men alle disse løsningene var i prinsippet like; iterer over alle tall mellom 0 og 1000, og filtrer ut og pluss sammen tallene som er multipler av 3 eller 5.
Jeg klarer ikke helt å slippe denne oppgaven. Alternativt kan vi nemlig se på det som et matematisk sett-problem, og da kan vi implementere løsninger som er litt mere deklerative. Hvis A er alle tall som er multipler av 3, og B er alle tall som er multipler av 5, så er løsningen å summere tallene i unionen av A og B.
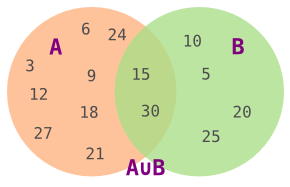
La oss ta en titt på ulike måter å implementere dette på...
Gitt at A og B er settene som beskrevet over. Da er en løsning å legge sammen summen av tallene i A og summen av tallene i B. Problemet nå er at tall som både er multipler av A og multipler av B blir lagt til i summen to ganger. For å løse dette kan vi trekke fra summen av alle disse tallene – nemlig alle tall som er multipler av 3 ganger 5, altså 15.
Her er en løsning i Ruby:
10 def sum_multiples args 11 (args[:of]..args[:upto]). 12 step(args[:of]). 13 reduce(:+) 14 end 15 16 sum = sum_multiples :of => 3, :upto => 999 17 sum += sum_multiples :of => 5, :upto => 999 18 sum -= sum_multiples :of => 3*5, :upto => 999 19 puts sum
Jeg liker hvor leselig koden blir: "Sum er lik sum multiples av 3 opp til 999" osv. Men ved å introdusere litt kodeduplisering kan det hele selvsagt gjøres endel enklere:
23 puts (3..999).step(3).reduce(:+) + 24 (5..999).step(5).reduce(:+) - 25 (3*5..999).step(3*5).reduce(:+)
Det vi trekker fra på slutten er altså snittet mellom A og B.
Mange programmeringsspråk/standard bibloteker har direkte støtte for å beregne unionen av to sett, og det kan vi også benytte. Her er en tilsvarende Ruby-implementasjon som oppretter A og B, tar unionen av disse, og summerer sammen:
30 def set args 31 (args[:of]..args[:upto]). 32 step(args[:of]). 33 to_a 34 end 35 36 multiples_of_3 = set :of => 3, :upto => 999 37 multiples_of_5 = set :of => 5, :upto => 999 38 multiples_of_3_or_5 = multiples_of_3 | multiples_of_5 39 40 puts multiples_of_3_or_5.reduce(:+)
Nå begynner det å komme seg :) Som en referanse slenger jeg med den samme løsningen implementert i Clojure, som har en egen set-datatype:
1 (defn multiples_of [x upto] 2 (set (range x upto x))) 3 4 (defn multiples_of_3_or_5 [] 5 (clojure.set/union (multiples_of 3 1000) 6 (multiples_of 5 1000))) 7 8 (->> (multiples_of_3_or_5) (reduce +) println)
Som du forstår er det mange ulike måter å løse en programmeringsoppgave på – selv en så enkel oppgave som dette. Ulike språk foretrekker ulike løsninger, og det er en av grunnene til at det er interessant å studere dem.
NÅ er det på tide å gi seg! Håper jeg ikke har kjedet vettet av deg med denne oppgaven – men nå er du i alle fall skikkelig primet og klar til å studere løsninger programmert i diverse språk du sansynligvis aldri har sett før. Neste blogpost kommer 1. desember!