Parallellisering av en algoritme i Erlang

tirsdag 4. mai 2010 Erlang Samtidighet

I denne blogposten får du se seks ulike løsninger på den aller enkleste oppgaven på Project Euler (jeg har snakket om hvordan jeg har brukt Euler til å lære meg nye programmeringsspråk her). Underveis vil du lære litt elementær Erlang-kode, se hvordan man kan parallellisere en enkel algoritme, og se hvilke ytelsesforbedringer det kan gi. Som en appetizer, her er ytelsen (forbrukt tid) på de ulike algoritmene relativt til hverandre:

Og her er oppgaven…

Project Euler : Problem 1
Hvis vi lister alle naturlige tall under 10 som er multipler av 3 eller 5, så får vi 3, 5, 6 og 9. Summen av disse er 23. Finn summen av alle multipler av 3 eller 5 under 1000.

Version 1 : tail recursion

For å finne løsningen kaller vi først sum-funksjonen i linje 4 med grenseverdien (1000 ifølge oppgaven). Dette vil kalle sum-funksjonen definert i linje 7 til 14 med verdiene 1000, 1 og 0 (Limit, Current og Sum). Linje 7 sier i praksis at hvis Limit og Current er like (de to første verdiene) så skal vi bare returnere Sum (som er svaret på oppgaven). Hvis vi ikke har kommet dit enda skal vi først sjekke om Current skal inkluderes i summen, og legger den til hvis den skal det, før vi øker Current og kaller sum igjen.

version_1.erl:

1 -module(version_1).
2 -export([sum/1]).
3
4 sum(Limit) ->
5 sum(Limit, 1, 0).
6
7 sum(Limit, Limit, Sum) -> Sum;
8 sum(Limit, Current, Sum) ->
9 case should_include(Current) of
10 true -> Sum1 = Sum + Current;
11 false -> Sum1 = Sum
12 end,
13 Next = Current + 1,
14 sum(Limit, Next, Sum1).
15
16 should_include(Number) ->
17 is_multiple_of(5, Number)
18 orelse
19 is_multiple_of(3, Number).
20
21 is_multiple_of(Factor, Number) ->
22 ((Number rem Factor) =:= 0).

Denne algoritmen er altså en rekursjon, eller mer presist en hale-rekursjon (fordi det siste som skjer i sum er at den kaller seg selv). Funksjonelle språk som Erlang er optimalisert for hale-rekursjon, og det vil ikke kunne gi stack overflow, slik språk som C# vil kunne gjøre om rekursjonen er for dyp.

Version 2 : Bruk av lists modulen

Etter å ha lært meg litt mer om mulighetene i Erlang fikk jeg lyst til å lage en versjon til av denne algoritmen. Det finnes nemlig en modul som heter lists som inneholder mange, greie funksjoner. Ved å kombinere seq, filter og sum derfra presterte jeg følgende, lille funksjonen som gav samme resultat.

version_2.erl:

1 -module(version_2).
2 -export([sum/1]).
3
4 sum(Limit) ->
5 lists:sum(
6     lists:filter(
7       fun(X) -> ((X rem 3) =:= 0) orelse ((X rem 5) =:= 0) end,
8       lists:seq(1, Limit)
9     )
10 ).

Lists:seq(1, 1000) gir meg en liste med alle tallene fra 1 til 1000. Ved å bruke filter-funksjonen kan jeg så sortere ut alle tallene jeg er interessert i. Linje 7 er forøvrig en lambda (anonym metode). Lists:sum summerer tallene i listen.

Versjon 2 er jo mye mindre, men er den bedre? Til å finne løsningen når Limit er 1000 er denne algoritmen helt utmerket. Den yter derimot dårligere om jeg øker Limit (betydelig), fordi den genererer en lang liste – og den listen må holdes i minne. Version 1 holdt jo bare selve summen i minne, og modifiserte den for hvert tall. Når Limit er stor nok bryter faktisk versjon 2 helt sammen.

Version 3 : List comprehension (med custom range)

Erlang er det første programmeringsspråket jeg har lært meg hvor jeg kan bruke list comprehensions (LINQ i C# er et lignende konsept), og denne oppgaven kan også løses med en sånn. Versjon 3 er ekvivalent med versjon 2 – uttrykket er i praksis et filter over en liste. I denne versjonen genererer jeg derimot min egen range i stedet for å bruke lists:seq.

version_3.erl:

1 -module(version_3).
2 -export([sum/1]).
3
4 sum(Limit) ->
5 lists:sum(
6 [ X || X <- range(1, Limit, []),
7 ((X rem 3) =:= 0) orelse ((X rem 5) =:= 0)]
8 ).
9
10 range(To, To, L) -> L;
11 range(From, To, L) -> range(From + 1, To, [From|L]).
12

Versjon 3 har samme problem som forrige versjon i forhold til å bryte sammen om Limit blir alt for stor. Den er derimot mye raskere enn begge de foregående algoritmene (ytelses-måling dokumentert lengre nede).

Version 4 : List comprehension (med lists:seq)

Siden versjon 3 fungerte så bra måtte jeg teste den med bruk av lists:seq også, og den viste seg faktisk å være enda raskere. Lists:seq er altså ikke noe problem.., det var nok lists:filter som gav dårlig performance i versjon 2.

version_4.erl:

1 -module(version_4).
2 -export([sum/1]).
3
4 sum(Limit) ->
5 lists:sum(
6 [X || X <- lists:seq(1, Limit),
7 ((X rem 3) =:= 0) orelse ((X rem 5) =:= 0)]
8 ).

Version 5 : Parallellisering av version 1

Denne oppgaven er perfekt for parallellisering – den er det vi kaller "pinlig parallelliserbar". Og siden Erlang er laget for parallellitet måtte jeg jo forsøke..

Alle algoritmene for å løse denne oppgaven tar i bunn og grunn en lang rekke tall og summerer dem sammen. Hvis man splitter opp den lange rekken i mindre deler, kan del-summen kalkuleres parallelt. Til slutt slår man sammen del-summene.

splitt_oppgaven2

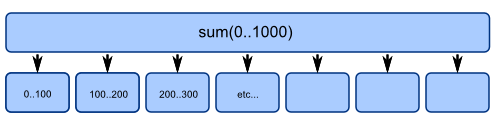
Mitt første forsøk på en parallell løsning er en kopi av versjon 1, hvor jeg oppretter ulike Erlang-prosesser for å finne summen for ulike intervaller, for så å samle sammen alle svarene. Linje 30 til 44 er mer eller mindre identisk med Versjon 1. I linje 28 sender en worker-prosess en melding tilbake til "master" med del-summen den har kommet frem til. Resten av koden oppretter worker-prosessene og samler sammen svarene.

version_5.erl:

1 -module(version_5).
2 -export([sum/2]).
3
4 sum(Limit, ProcCount) when Limit >= ProcCount ->
5 BulkSize = Limit div ProcCount,
6 RealProcCount = ProcCount + (if (Limit rem BulkSize) > 0 -> 1; true -> 0 end),
7 spawn_workers(self(), Limit, 1, BulkSize),
8 collect_replies(0, RealProcCount).
9
10 collect_replies(Total, 0)                 -> Total;
11 collect_replies(Total, RemainingMessages) ->
12 receive
13     {sum, Subsum} ->
14       collect_replies(Total + Subsum, RemainingMessages - 1)
15 end.
16
17 spawn_workers(Master, Limit, Current, BulkSize)
18 when Limit > (Current + BulkSize) ->
19 Next = Current + BulkSize,
20 spawn(fun() -> worker(Next, Current, 0, Master) end),
21 spawn_workers(Master, Limit, Next, BulkSize);
22
23 spawn_workers(Master, Limit, Current, _) ->
24 Rest = Limit - Current,
25 spawn(fun() -> worker(Rest + Current, Current, 0, Master) end).
26
27 worker(Limit, Limit, Sum, Master) ->
28 Master ! {sum, Sum};
29
30 worker(Limit, Current, Sum, Master) ->
31 case should_include(Current) of
32     true -> Sum1 = Sum + Current;
33     false -> Sum1 = Sum
34 end,
35 Next = Current + 1,
36 worker(Limit, Next, Sum1, Master).
37
38 should_include(Number) ->
39 is_multiple_of(5, Number)
40 orelse
41 is_multiple_of(3, Number).
42
43 is_multiple_of(Factor, Number) ->
44 ((Number rem Factor) =:= 0).

Om jeg kjører denne parallelle utgaven av den orginale algoritmen på min arbeidsmaskin, og spesifiserer at den skal bruke 2 prosesser (altså dele arbeidet i to), så blir den nesten dobbelt så rask. Den bruker like mye CPU-tid som før, men arbeidet fordeles over mine to prosessorer, og svaret dukker derfor opp dobbelt så raskt (kun med et lite overhead for å administrere prosessene).

Noen forbedring utover dette klarer jeg derimot ikke å oppnå – ikke på min maskin. Hadde jeg hatt flere CPU'er ville jeg fått en høyere effekt om jeg splittet opp arbeidet ytterligere.

Version 6 : Parallellisering av version 4

Men jeg hadde fortsatt et håp om å få bedre utbytte av parallellitet, så jeg lagde en parallell utgave av versjon 4 også, den raskeste av de sekvensielle algoritmene. Denne gangen inneholder koden ikke noe nytt – denne er en kombinasjon av version 4 og 5..

version_6.erl:

1 -module(version_6).
2 -export([sum/2]).
3
4 sum(Limit, ProcCount) when Limit >= ProcCount ->
5 BulkSize = Limit div ProcCount,
6 RealProcCount = ProcCount + (if (Limit rem BulkSize) > 0 -> 1; true -> 0 end),
7 spawn_workers(self(), Limit, 1, BulkSize),
8 collect_replies(0, RealProcCount).
9
10 collect_replies(Total, 0)                 -> Total;
11 collect_replies(Total, RemainingMessages) ->
12 receive
13     {sum, Subsum} ->
14       collect_replies(Total + Subsum, RemainingMessages - 1)
15 end.
16
17 spawn_workers(Master, Limit, Current, BulkSize)
18 when Limit > (Current + BulkSize) ->
19 Next = Current + BulkSize,
20 spawn(fun() -> worker(Current, Next, Master) end),
21 spawn_workers(Master, Limit, Next, BulkSize);
22
23 spawn_workers(Master, Limit, Current, _) ->
24 Rest = Limit - Current,
25 spawn(fun() -> worker(Current, Rest + Current, Master) end).
26
27 worker(BatchStart, BatchEnd, Master) ->
28 Sum = lists:sum(
29     [X || X <- lists:seq(BatchStart, BatchEnd - 1),
30       ((X rem 3) =:= 0) orelse ((X rem 5) =:= 0)]
31 ),
32 Master ! {sum, Sum}.

Denne implementasjonen oppførte seg ganske anderledes; når den ble kjørt med et lavt antall prosesser var den ikke spesielt bra, i alle fall ikke for høye verdier av Limit, ettersom den holder listene i minne. Men etterhvert som jeg skrudde opp antall prosesser gikk prosesseringstiden ned betydelig. Det jeg kunne observere her var at samtidig som jeg utnyttet mine to prosessorer så gikk også den totale CPU-tiden ned fordi listene blir mindre når intervallet blir delt nok opp.

Resultater

En Limit på 1000 er for lite til å observere noen tydelig forskjell mellom algoritmene. 20 millioner gir derimot et greit utslag. Her følger er reell sammenligning av alle versjonene med 20000000 som Limit.

6> problem1:test(20000000).
'Version 1' calculates sum 93333316666668 in 4212 (4353) ms
'Version 2' calculates sum 93333336666668 in 4805 (5990) ms
'Version 3' calculates sum 93333316666668 in 2590 (3120) ms
'Version 4' calculates sum 93333336666668 in 2402 (2824) ms
'Version 5 (   1 proc )' calculates sum 93333316666668 in 4602 (4695) ms
'Version 5 (   2 procs)' calculates sum 93333316666668 in 4789 (2543) ms
'Version 5 (   5 procs)' calculates sum 93333316666668 in 4852 (2543) ms
'Version 5 (  10 procs)' calculates sum 93333316666668 in 4836 (2496) ms
'Version 5 ( 100 procs)' calculates sum 93333316666668 in 4758 (2527) ms
'Version 5 (1000 procs)' calculates sum 93333316666668 in 4914 (3074) ms
'Version 6 (   1 proc )' calculates sum 93333316666668 in 4274 (5990) ms
'Version 6 (   2 procs)' calculates sum 93333316666668 in 4509 (3744) ms
'Version 6 (   5 procs)' calculates sum 93333316666668 in 4524 (3167) ms
'Version 6 (  10 procs)' calculates sum 93333316666668 in 3619 (2543) ms
'Version 6 ( 100 procs)' calculates sum 93333316666668 in 2980 (1965) ms
'Version 6 (1000 procs)' calculates sum 93333316666668 in 2667 (1513) ms
'Version 6 (5000 procs)' calculates sum 93333316666668 in 2777 (1607) ms

Det første tallet for hver kjøring er CPU-tid, mens tallet i parantes er faktisk klokketid – begge i millisekunder. Legg merke til at begge de parallelle algoritmene begynner å "slite" om det opprettes for mange prosesser. Dette er naturlig fordi det er et overhead knyttet til å administrere og veksle mellom dem. 5000 processer er dog helt uproblematisk for version 6, selv om det optimale er nærmere 1000.

For å teste algoritmene brukte jeg følgende script..

problem1.erl:

1 -module(problem1).
2 -export([test/1]).
3
4 test(Limit) ->
5 compile([version_1, version_2, version_3, version_4, version_5, version_6]),
6 run('Version 1', fun() -> version_1:sum(Limit) end),
7 run('Version 2', fun() -> version_2:sum(Limit) end),
8 run('Version 3', fun() -> version_3:sum(Limit) end),
9 run('Version 4', fun() -> version_4:sum(Limit) end),
10 run('Version 5 (   1 proc )', fun() -> version_5:sum(Limit, 1) end),
11 run('Version 5 (   2 procs)', fun() -> version_5:sum(Limit, 2) end),
12 run('Version 5 (   5 procs)', fun() -> version_5:sum(Limit, 5) end),
13 run('Version 5 ( 10 procs)', fun() -> version_5:sum(Limit, 10) end),
14 run('Version 5 ( 100 procs)', fun() -> version_5:sum(Limit, 100) end),
15 run('Version 5 (1000 procs)', fun() -> version_5:sum(Limit, 1000) end),
16 run('Version 6 (   1 proc )', fun() -> version_6:sum(Limit, 1) end),
17 run('Version 6 (   2 procs)', fun() -> version_6:sum(Limit, 2) end),
18 run('Version 6 (   5 procs)', fun() -> version_6:sum(Limit, 5) end),
19 run('Version 6 ( 10 procs)', fun() -> version_6:sum(Limit, 10) end),
20 run('Version 6 ( 100 procs)', fun() -> version_6:sum(Limit, 100) end),
21 run('Version 6 (1000 procs)', fun() -> version_6:sum(Limit, 1000) end),
22 run('Version 6 (5000 procs)', fun() -> version_6:sum(Limit, 5000) end).
23
24 compile(Scripts) ->
25 lists:foreach(fun(X) -> c:c(X) end, Scripts).
26
27 run(Label, Fun) -> % run the function, measure and report times
28 statistics(runtime),
29 statistics(wall_clock),
30 Sum = Fun(),
31 {_, Time1} = statistics(runtime),
32 {_, Time2} = statistics(wall_clock),
33 io:format("~p calculates sum ~p in ~p (~p) ms~n",
34     [Label, Sum, Time1, Time2]).

ADVARSEL!!!
Etter å ha skrevet denne artikkelen oppdaget jeg desverre at koden inneholdt noen feil - feil som åpenbarte seg når testene ble kjørt med visse "grenseverdier". De har ikke så stor betydning at de negerer det jeg forklarer i blogposten, men noe du bør være klar over om du studerer algoritmene i detalj, spesielt versjon 5 og 6, eller om du ønsker å kjøre dem selv. Kudos til dem som ønsker/klarer å påpeke feilene, og kanskje også vise hvordan de skal fikses. Dere selvsagt velkomne til det i kommentarfeltet.